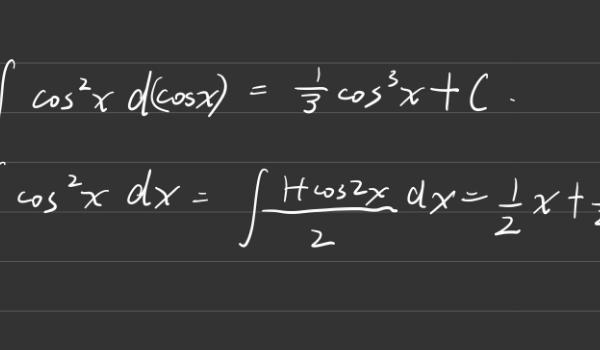cosx的平方:深入理解与应用
在三角函数中,cosx(余弦函数)是一个基础且重要的概念,而cosx的平方则在此基础上进一步拓展了数学和物理领域的应用。本文将深入探讨cosx的平方的性质、计算方法及其在实际问题中的应用。
一、cosx的平方的定义与性质
cosx的平方,即(cosx)^2,表示余弦函数值的平方。在数学上,它有着独特的性质:
- 周期性:由于cosx本身具有周期性(周期为2π),因此cosx的平方也具有相同的周期性。
- 对称性:cosx的平方是偶函数,即(cos(-x))^2 = (cosx)^2,图像关于y轴对称。
- 值域范围:cosx的值域为[-1,1],因此(cosx)^2的值域为[0,1]。
二、cosx的平方的计算方法
计算cosx的平方,最直接的方法是先求出cosx的值,然后将其平方。但在某些特定情境下,可以利用三角恒等式或积分技巧来简化计算过程。
- 直接计算法:对于给定的x值,使用计算器或查表法求出cosx,然后计算其平方。
- 三角恒等式法:利用三角恒等式,如cos^2x = (1 + cos2x)/2,可以更方便地计算cosx的平方,特别是在处理涉及倍角公式的问题时。
- 积分法:在积分运算中,cosx的平方经常作为被积函数出现,此时可以利用积分技巧求解。
三、cosx的平方的应用
cosx的平方在多个领域有着广泛的应用,包括但不限于物理学、工程学、信号处理等。
1. 物理学中的应用
在物理学中,cosx的平方常用于描述波动现象,如光的干涉和衍射。在光学中,光强分布与cosx的平方密切相关,通过计算cosx的平方可以预测光强的分布规律。
2. 工程学中的应用
在结构工程中,cosx的平方用于分析梁的弯曲变形。通过计算梁在受力作用下的cosx的平方分布,可以评估梁的强度和稳定性。
3. 信号处理中的应用
在信号处理领域,cosx的平方用于分析信号的频谱特性。特别是在傅里叶变换中,cosx的平方作为基函数之一,对于信号的分解和重构具有重要意义。
“cosx的平方不仅是数学上的一个简单概念,更是连接理论与实践的桥梁。通过深入理解其性质和应用,我们可以更好地解决实际问题。”
四、结论
cosx的平方作为三角函数的一个重要组成部分,具有独特的性质和广泛的应用。通过本文的介绍,我们希望能够为读者提供一个全面而深入的理解,以便在实际问题中灵活运用这一数学概念。
未来,随着科学技术的不断发展,cosx的平方的应用领域还将进一步拓展。我们期待更多的学者和工程师能够关注这一领域,共同推动数学与物理、工程等学科的交叉融合。