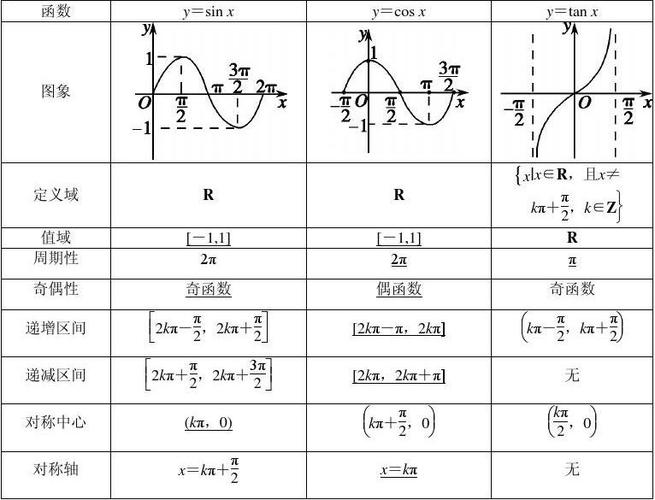
cos函数图像:深入解析与视觉探索
在数学的广阔天地里,三角函数占据着举足轻重的地位,其中cos函数(余弦函数)作为三角函数家族的重要成员,其图像不仅美观而且蕴含了丰富的数学意义。本文将带您深入探索cos函数图像的特点、绘制方法以及其在各个领域的应用。
cos函数的基本定义
cos函数,全称为余弦函数,是三角函数的一种。对于任意实数x,cos(x)表示单位圆上,与x轴正方向夹角为x的点的x坐标。其数学表达式为:
cos(x) = 邻边/斜边
在直角三角形中,cos函数描述了邻边与斜边之间的比值关系。
cos函数图像的特点
cos函数图像是一个周期函数图像,其周期为2π。这意味着图像在x轴上每隔2π就会重复一次。cos函数图像呈现出一种波浪形,最高点为1,最低点为-1,且关于y轴对称。
- 周期性:cos函数的周期为2π,意味着图像在x轴上每隔2π就会重复一次。
- 对称性:cos函数图像关于y轴对称,即对于任意实数x,都有cos(-x) = cos(x)。
- 极值点:在x = 0, ±π, ±2π,…处,cos函数取得极值,其中在x = 0, ±2π,…处取得最大值1,在x = ±π, ±3π,…处取得最小值-1。
绘制cos函数图像的方法
绘制cos函数图像可以通过多种方法实现,包括手工绘制、使用数学软件或编程语言等。
- 手工绘制:在坐标系中,选择一系列x值,计算对应的cos(x)值,然后在坐标系中标出这些点,最后用平滑的曲线连接这些点即可得到cos函数图像。
- 使用数学软件:如GeoGebra、Desmos等,这些软件提供了强大的绘图功能,只需输入cos函数表达式,即可自动生成图像。
- 编程语言:如Python的matplotlib库、JavaScript的D3.js等,通过编写代码可以精确控制图像的绘制过程,实现更复杂的视觉效果。
实例:使用Python绘制cos函数图像
以下是一个使用Python的matplotlib库绘制cos函数图像的简单示例:
import matplotlib.pyplot as plt
import numpy as np
# 生成x值
x = np.linspace(-2*np.pi, 2*np.pi, 1000)
# 计算cos(x)值
y = np.cos(x)
# 绘制图像
plt.plot(x, y)
plt.title('cos函数图像')
plt.xlabel('x')
plt.ylabel('cos(x)')
plt.grid(True)
plt.show()
cos函数图像的应用
cos函数图像在多个领域都有着广泛的应用,包括但不限于物理学、工程学、信号处理等。
- 物理学:在简谐振动中,物体的位移随时间的变化关系可以用cos函数来描述。
- 工程学:在交流电路中,电压和电流随时间的变化关系也常用cos函数来表示。
- 信号处理:在信号处理领域,cos函数常用于生成和分析周期性信号。
结语
cos函数图像作为三角函数图像的重要组成部分,不仅具有独特的数学美感,还在多个领域发挥着重要作用。通过深入探索cos函数图像的特点、绘制方法以及应用,我们可以更好地理解这一数学工具的价值和意义。