arcsinx图像:深入解析与应用实例
在数学和物理学中,反三角函数是一类重要的函数,它们用于解决涉及角度和边长的问题。其中,arcsinx(反正弦函数)是反三角函数家族中的一员,本文将详细探讨arcsinx的图像特征、性质以及在实际问题中的应用。
一、arcsinx图像的基本特征
arcsinx函数,记作y = arcsin(x),其定义域为[-1, 1],值域为[-π/2, π/2]。这意味着,对于任何在-1到1之间的x值,arcsinx都能给出一个在-π/2到π/2之间的y值,这个y值对应于sin(y) = x的角度。
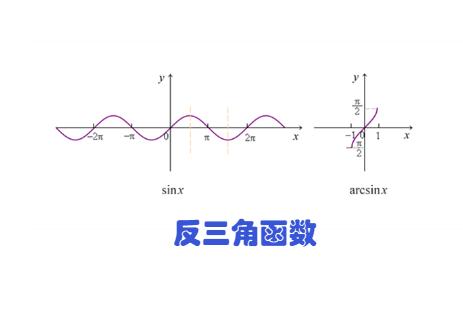
arcsinx的图像呈现为一个在原点对称的S形曲线。具体来说:
- 当x = -1时,y = -π/2;
- 当x = 0时,y = 0;
- 当x = 1时,y = π/2。
在定义域内,arcsinx是单调递增的,这意味着随着x的增大,y也相应增大。
二、arcsinx图像的性质
1. 奇函数性质:arcsinx是奇函数,即满足arcsin(-x) = -arcsin(x)。这意味着图像关于原点对称。
2. 导数性质:arcsinx的导数为1/√(1-x²)。这表明在定义域内,arcsinx的斜率随着x的增大而减小,但始终为正。
3. 渐近线:虽然arcsinx没有垂直渐近线,但它在x = -1和x = 1处水平渐近于y = -π/2和y = π/2。
三、arcsinx图像的应用实例
arcsinx函数在多个领域有着广泛的应用,包括但不限于物理学、工程学和经济学。
1. 物理学中的应用
在物理学中,arcsinx常用于解决涉及角度和力的问题。例如,在力学中,当知道一个物体在某一方向上的分力时,可以通过arcsinx计算出该分力与合力之间的夹角。
2. 工程学中的应用
在工程学中,arcsinx函数常用于信号处理、控制系统和电路设计等领域。例如,在信号处理中,可以通过arcsinx函数对信号进行非线性变换,以实现特定的滤波效果。
3. 经济学中的应用
在经济学中,arcsinx函数可以用于分析市场供需关系、预测价格变动等。例如,在供需模型中,可以通过arcsinx函数来描述价格与需求量之间的非线性关系。
四、结论
arcsinx图像作为反正弦函数的直观表示,具有独特的S形曲线特征和丰富的数学性质。通过深入了解arcsinx图像的特征和性质,我们可以更好地理解和应用这一函数,解决各种实际问题。无论是在物理学、工程学还是经济学等领域,arcsinx都发挥着不可替代的作用。
“数学是科学的皇后,而反三角函数则是皇后手中的权杖。” —— 未知
希望本文能够帮助读者更深入地了解arcsinx图像及其在实际问题中的应用。