随机梯度下降:优化机器学习模型的利器
在机器学习的广阔领域中,优化算法扮演着至关重要的角色。它们负责调整模型的参数,以最小化损失函数,从而提高模型的预测性能。在众多优化算法中,随机梯度下降(Stochastic Gradient Descent, SGD)无疑是最为经典且广泛使用的一种。本文将深入探讨随机梯度下降的原理、实现方式、优缺点以及其在现代机器学习中的应用。
一、随机梯度下降的原理
随机梯度下降是一种迭代优化算法,旨在通过逐步调整模型参数来最小化损失函数。与传统的梯度下降算法相比,SGD在每次迭代中仅使用一个训练样本来计算梯度,而不是使用整个训练集。这种做法大大加快了训练速度,尤其是在处理大规模数据集时。
SGD的基本步骤如下:
- 随机选择一个训练样本。
- 计算该样本对应的损失函数关于模型参数的梯度。
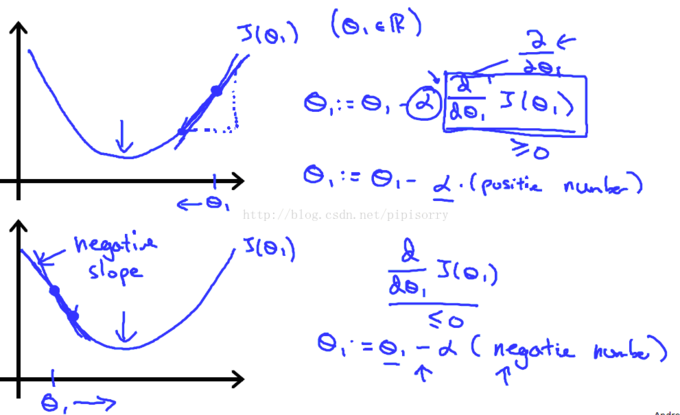
- 根据梯度方向更新模型参数,通常使用以下公式:
θ = θ – η * ∇L(θ)
其中,θ表示模型参数,η是学习率,∇L(θ)是损失函数关于θ的梯度。 - 重复上述步骤,直至满足停止条件(如达到预设的迭代次数或损失函数值小于某个阈值)。
二、随机梯度下降的实现方式
SGD有多种实现方式,包括标准SGD、小批量SGD(Mini-batch SGD)等。标准SGD每次迭代只使用一个样本,而小批量SGD则使用一个小批量(即多个样本)来计算梯度。小批量SGD通常能够在保持较快训练速度的同时,减少梯度估计的方差,从而提高算法的稳定性。
小批量SGD的伪代码示例:
初始化模型参数θ和学习率η
对于每个epoch:
打乱训练集
对于每个小批量b:
计算小批量b的损失函数L(θ)
计算梯度∇L(θ)
更新模型参数:θ = θ – η * ∇L(θ)
三、随机梯度下降的优缺点
优点:
- 计算效率高:每次迭代只需处理一个或少数几个样本,大大加快了训练速度。
- 适用于大规模数据集:由于每次迭代只涉及少量样本,SGD能够处理包含数百万甚至数十亿样本的数据集。
- 具有一定的泛化能力:由于引入了随机性,SGD有助于模型跳出局部最优解,从而找到更好的全局最优解。
缺点:
- 梯度估计的方差较大:由于每次迭代只使用一个或少数几个样本,SGD的梯度估计可能不够准确,导致模型参数更新不稳定。
- 学习率的选择较为困难:学习率过大可能导致模型无法收敛,学习率过小则可能导致训练过程过于缓慢。
四、随机梯度下降在现代机器学习中的应用
SGD及其变种(如小批量SGD、动量SGD、Adam等)在现代机器学习中得到了广泛应用。它们被用于训练各种模型,包括线性回归、逻辑回归、神经网络等。特别是在深度学习领域,SGD及其优化算法成为了训练大规模神经网络的标准工具。
此外,随着硬件技术的发展和算法的不断优化,SGD的性能也在不断提升。例如,使用GPU加速SGD的计算过程,可以进一步缩短训练时间;通过引入动量、RMSprop、Adam等优化技术,可以进一步提高SGD的稳定性和收敛速度。
结语
随机梯度下降作为一种经典的优化算法,在机器学习和深度学习中发挥着重要作用。尽管它存在一些缺点,但通过不断的技术创新和算法优化,SGD的性能和应用范围仍在不断拓展。未来,随着大数据和人工智能技术的不断发展,SGD及其变种将继续在机器学习领域发挥重要作用。