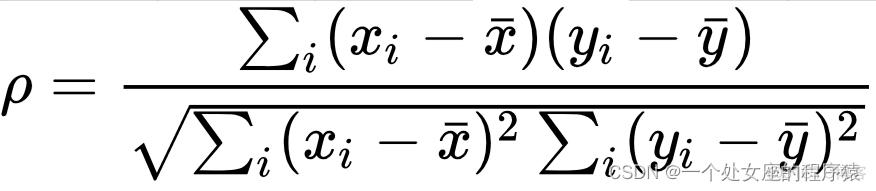斯皮尔曼相关系数:深入解析与应用
斯皮尔曼相关系数,也称为斯皮尔曼秩相关系数,是一种非参数的统计方法,用于衡量两个变量之间的单调关系强度与方向。本文将详细探讨斯皮尔曼相关系数的定义、计算方法、适用范围、特点及其在各个领域的应用。
一、斯皮尔曼相关系数的定义
斯皮尔曼相关系数是一种非参数的秩相关系数,它通过数据等级而非原始数值来计算两个变量之间的相关性。其核心在于将每个变量的观测值转换为等级(秩),然后计算这些等级之间的差异,从而得出两个变量之间的相关程度。斯皮尔曼相关系数的取值范围在-1到1之间,其中1表示完全正相关,-1表示完全负相关,0表示无线性相关。
二、斯皮尔曼相关系数的计算方法
斯皮尔曼相关系数的计算过程可以分为以下几个步骤:
- 将两个变量的数据按照数值大小进行排序。
- 给每个数据点分配一个等级,等级通常从1开始。如果两个或多个数值相同,则给它们分配相同的平均等级。
- 计算每个变量的等级之间的差异,然后根据这些差异计算斯皮尔曼相关系数。
例如,假设我们有以下两组数据:
- X: 3, 8, 4, 7, 2
- Y: 5, 10, 9, 6, 1
首先,我们将数据按照大小排序:
- 排序后的X: 2, 3, 4, 7, 8
- 排序后的Y: 1, 5, 6, 9, 10
然后,给每个数据点分配等级:
- 等级X: 1, 2, 3, 4, 5
- 等级Y: 1, 2, 3, 4, 5
最后,根据等级差异计算斯皮尔曼相关系数。
三、斯皮尔曼相关系数的适用范围
斯皮尔曼相关系数适用于非线性关系的评估,因为它衡量的是单调关系,而不仅仅是线性关系。此外,斯皮尔曼相关系数对异常值和数据分布形态不敏感,因此适用于非正态分布、异常值较多或有序分类数据的情况。
四、斯皮尔曼相关系数的特点
斯皮尔曼相关系数具有以下几个特点:
- 非参数性:斯皮尔曼相关系数不依赖于变量的分布情况,因此适用于非参数统计分析。
- 单调性:斯皮尔曼相关系数衡量的是两个变量之间的单调关系,即一个变量增加时,另一个变量也增加(单调正相关)或减少(单调负相关)。
- 鲁棒性:斯皮尔曼相关系数对异常值和数据分布形态不敏感,因此具有更好的鲁棒性。
五、斯皮尔曼相关系数的应用
斯皮尔曼相关系数被广泛应用于各种研究领域,包括社会科学、自然科学等。例如,在社会科学中,可以使用斯皮尔曼相关系数来研究收入与教育水平之间的关系;在自然科学中,可以使用斯皮尔曼相关系数来研究气温与降雨量之间的关系。
实际应用案例
假设我们要研究市场需求与产品销量之间的关系,可以使用斯皮尔曼相关系数来判断两个变量是否有相关性。如果相关系数接近1或-1,那么可以认为市场需求与产品销量之间存在较强的线性关系;如果相关系数接近0,则意味着市场需求与产品销量之间的关系较弱或者没有线性关系。
六、总结
斯皮尔曼相关系数是一种非参数统计方法,用于衡量两个变量之间的单调关系强度与方向。它通过数据等级而非原始数值来计算相关性,适用于非线性关系、异常值较多或有序分类数据的情况。在实际应用中,斯皮尔曼相关系数被广泛应用于各个领域,为研究人员提供了有力的分析工具。