二叉树的遍历：深度解析与实现方法

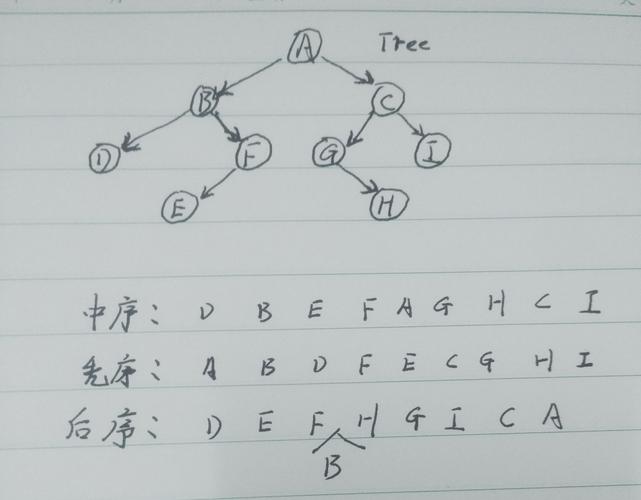
二叉树的遍历：深度解析与实现方法

在计算机科学中，二叉树是一种重要的数据结构，广泛应用于各种算法和数据结构中。遍历二叉树是理解和操作二叉树的基础，本文将详细探讨二叉树的遍历方法，包括前序遍历、中序遍历、后序遍历和层次遍历，并提供相应的实现代码。

一、二叉树的基本概念

二叉树是一种树形数据结构，其中每个节点最多有两个子节点，通常称为左子节点和右子节点。二叉树可以是空树，也可以由一个根节点和左右两个子树构成。

二、二叉树的遍历方法

1. 前序遍历（Preorder Traversal）

前序遍历的顺序是：访问根节点 -> 遍历左子树 -> 遍历右子树。这种遍历方式常用于构建二叉树的表达式树。

实现代码（Python）：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def preorderTraversal(root):
    if root is None:
        return []
    return [root.val] + preorderTraversal(root.left) + preorderTraversal(root.right)

2. 中序遍历（Inorder Traversal）

中序遍历的顺序是：遍历左子树 -> 访问根节点 -> 遍历右子树。这种遍历方式常用于二叉搜索树的排序。

实现代码（Python）：

def inorderTraversal(root):
    if root is None:
        return []
    return inorderTraversal(root.left) + [root.val] + inorderTraversal(root.right)

3. 后序遍历（Postorder Traversal）

后序遍历的顺序是：遍历左子树 -> 遍历右子树 -> 访问根节点。这种遍历方式常用于释放资源或删除节点。

实现代码（Python）：

def postorderTraversal(root):
    if root is None:
        return []
    return postorderTraversal(root.left) + postorderTraversal(root.right) + [root.val]

4. 层次遍历（Level Order Traversal）

层次遍历是按层次从上到下、从左到右依次访问每个节点。这种遍历方式常用于处理需要按层次操作的问题。

实现代码（Python）：

from collections import deque

def levelOrderTraversal(root):
    if root is None:
        return []
    result = []
    queue = deque([root])
    while queue:
        node = queue.popleft()
        result.append(node.val)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)
    return result

三、总结

二叉树的遍历是理解和操作二叉树的基础，不同的遍历方式适用于不同的应用场景。通过掌握前序遍历、中序遍历、后序遍历和层次遍历，我们可以更好地理解和利用二叉树这一数据结构。

希望本文能帮助读者深入理解二叉树的遍历方法，并在实际编程中灵活运用。