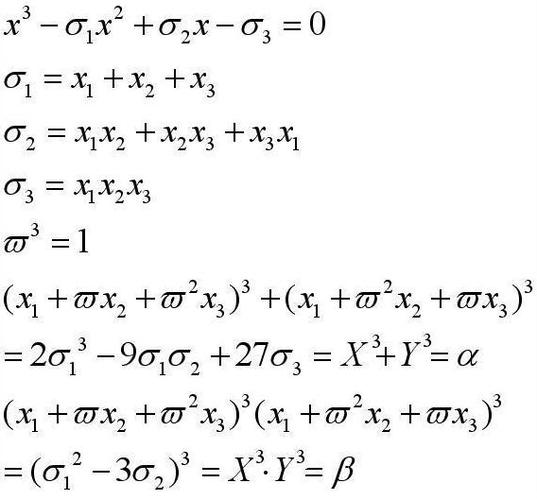一元三次方程求根公式
在数学领域,一元三次方程(Cubic Equation)是一种形式为 ax^3 + bx^2 + cx + d = 0 的方程,其中 a ≠ 0。求解这类方程的过程相对复杂,但幸运的是,数学家们已经找到了一个通用的求根公式,即卡尔丹公式(Cardano’s Formula)。本文将详细介绍这一公式及其应用。
卡尔丹公式简介
卡尔丹公式是求解一元三次方程的一种代数方法,它允许我们直接计算出方程的根,尽管计算过程可能相当繁琐。公式的基本形式如下:
设一元三次方程为 ax^3 + bx^2 + cx + d = 0,且令:
- Δ₀ = b² – 3ac
- Δ₁ = 2b³ – 9abc + 27a²d
- C = (Δ₁ + √(Δ₁² – 4Δ₀³)) / 2
- U = C^(1/3)
- V = Δ₀ / (3aU)
则方程的根为:
- x₁ = U + V – b / (3a)
- x₂ = ωU + ω²V – b / (3a)
- x₃ = ω²U + ωV – b / (3a)
其中 ω 是复数的单位根,满足 ω³ = 1,即 ω = -1/2 + √3/2i 或其共轭复数。
公式的应用步骤
- 计算判别式:首先计算 Δ₀ 和 Δ₁,这两个值将帮助我们判断方程的根的性质。
- 求解中间变量:根据 Δ₀ 和 Δ₁ 计算 C,然后求出 U 和 V。
- 应用公式求根:使用计算出的 U、V 和 b、a 的值,代入公式求出三个根 x₁、x₂ 和 x₃。
特殊情况处理
在实际应用中,一元三次方程可能具有一些特殊情况,如重根或实根等。这些情况需要特别处理:
- Δ₁ = 0:此时方程有一个重根和两个相等的实根,或者三个相等的实根。
- Δ₁² – 4Δ₀³ < 0:这种情况下,方程有一个实根和两个共轭复数根。
- Δ₁² – 4Δ₀³ = 0:此时方程有一个重根和一个单根,或者三个相等的实根(与 Δ₁ = 0 的情况重叠)。
实例演示
考虑方程 x³ – 6x² + 11x – 6 = 0,我们可以按照以下步骤求解:
- 计算判别式:Δ₀ = (-6)² – 3(1)(11) = 36 – 33 = 3,Δ₁ = 2(-6)³ – 9(1)(-6)(11) + 27(1)²(-6) = -432 + 594 – 162 = 0。
- 由于 Δ₁ = 0,方程有一个重根。此时,我们可以使用因式分解法或其他简化方法求解,或者直接应用卡尔丹公式(尽管在这种情况下可能不是最高效的方法)。
- 应用卡尔丹公式(略过具体计算,因为 Δ₁ = 0 时有更简单的方法),我们得到根为 x₁ = 1, x₂ = x₃ = 3。
结论
一元三次方程的求根公式——卡尔丹公式,虽然计算复杂,但为求解这类方程提供了一种通用的代数方法。通过仔细理解和应用这一公式,我们可以有效地解决各种一元三次方程问题。同时,对于特殊情况的处理也是求解过程中不可忽视的重要部分。